03.Pytorch张量数值计算

Leefs 2024-12-15 AM 75℃ 0条

[TOC]

### 一、张量基本运算

基本运算中，包括 `add`、`sub`、`mul`、`div`、`neg` 等函数, 以及这些函数的带下划线的版本 `add_`、`sub_`、`mul_`、`div_`、`neg_`，其中带**下划线的版本为修改原数据**。

| 操作类型           | 函数   | 示例代码                  | 代码解释                            |
| ------------------ | ------ | ------------------------- | ----------------------------------- |
| 加法(不修改原数据) | `add`  | `new_data = data.add(10)` | 将每个元素加上10，生成一个新张量。  |
| 加法(修改原数据)   | `add_` | `data.add_(10)`           | 将每个元素加上10，直接修改原数据。  |
| 减法               | `sub`  | `data.sub(100)`           | 将每个元素减去100，生成一个新张量。 |
| 乘法               | `mul`  | `data.mul(100)`           | 将每个元素乘以100，生成一个新张量。 |
| 除法               | `div`  | `data.div(100)`           | 将每个元素除以100，生成一个新张量。 |
| 取反               | `neg`  | `data.neg()`              | 将每个元素取反，生成一个新张量。    |

**代码示例**

```python
import torch

# 1. 不修改原数据的计算
def test01():

# 第一个参数: 开始值
    # 第二个参数: 结束值
    # 第三个参数: 形状
    data = torch.randint(0,10,[2,3])
    print(data)
    print('-' * 20)
    # 计算完成之后,会返回一个新的张量
    data = data.add(10)
    print(data)

# data.sub()      # 减法
    # data.mul()      # 乘法
    # data.div()      # 除法
    # data.neg()      # 取相反数

# 2. 修改原数据的计算(inplace方式的计算)
def test02():

data = torch.randint(0,10,[2,3])
    print(data)
    print('-' * 20)
    # 带下划线的版本的函数直接修改原数据,不需要用新的变量保存
    data.add_(10)
    print(data)

# data.sub_()      # 减法
    # data.mul_()      # 乘法
    # data.div_()      # 除法
    # data.neg_()      # 取相反数

if __name__ == '__main__':
    test01()
    print('-' * 50)
    test02()
```

**输出结果**

```
tensor([[0, 9, 8],
        [2, 5, 8]])
--------------------
tensor([[10, 19, 18],
        [12, 15, 18]])
--------------------------------------------------
tensor([[0, 2, 3],
        [5, 9, 2]])
--------------------
tensor([[10, 12, 13],
        [15, 19, 12]])
```

### 二、哈达玛积

哈达玛积（Hadamard Product），又称为元素积（element-wise product），是指两个相同尺寸的矩阵对应元素相乘得到的新矩阵。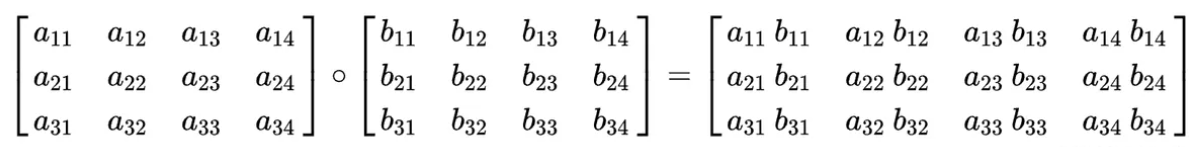

![03.Pytorch张量数值计算01.jpg](https://lilinchao.com/usr/uploads/2024/12/3118418416.jpg)

**哈达玛积与矩阵乘法不同，矩阵乘法是行与列的点积，而哈达玛积只是简单的元素相乘。**

**代码中哈达玛积计算有两种方法**:

+ **使用 `mul` 函数**

```python
  torch.mul(input, other, out=None)
  ```

- 功能：执行元素级乘法操作。
  - 输入：接受两个输入张量，并对它们的对应元素进行逐元素相乘。
  - 输出：返回一个新的张量，其中包含两个输入张量对应元素的乘积。

**参数说明**：

- input：输入张量。
  - other：用于逐元素相乘的张量。
  - out（可选）：输出张量，用于指定结果的存储位置。

+ **使用 `*` 号运算符**

**代码示例**

```python
import torch

# 1. 使用 mul 函数
def test01():

data1 = torch.tensor([[1,2],[3,4]])
    data2 = torch.tensor([[5,6],[7,8]])

data = torch.mul(data1,data2)
    # data = data1.mul(data2)
    print(data)

# 2. 使用 * 号运算符
def test02():

data1 = torch.tensor([[1,2],[3,4]])
    data2 = torch.tensor([[5,6],[7,8]])

data = data1 * data2
    print(data)
if __name__ == '__main__':
    test01()
    print('-' * 50)
    test02()
```

**输出结果**

```
tensor([[ 5, 12],
        [21, 32]])
--------------------------------------------------
tensor([[ 5, 12],
        [21, 32]])
```

### 三、点积运算

#### 3.1 概述

点积（Dot Product）是向量计算中的一种基本运算，它将两个向量对应元素相乘并求和。

点积在机器学习和深度学习中广泛应用于各种计算，如向量相似性、神经网络中的加权和计算等。

![03.Pytorch张量数值计算02.png](https://lilinchao.com/usr/uploads/2024/12/1182620604.png)

点积运算要求第一个矩阵 `shape: (n, m)`，第二个矩阵 `shape: (m, p)`, 两个矩阵点积运算 `shape 为: (n, p)`。

![03.Pytorch张量数值计算03.png](https://lilinchao.com/usr/uploads/2024/12/2795798102.png)

![03.Pytorch张量数值计算04.png](https://lilinchao.com/usr/uploads/2024/12/4042769518.png)

#### 3.2 运算方式

1. 运算符 `@` 用于进行两个矩阵的点乘运算
2. `torch.mm` 用于进行两个矩阵点乘运算, 要求输入的矩阵为2维
3. `torch.bmm` 用于批量进行矩阵点乘运算, 要求输入的矩阵为3维
4. `torch.matmul` 对进行点乘运算的两矩阵形状没有限定.
   1. 对于输入都是二维的张量相当于 mm 运算.
   2. 对于输入都是三维的张量相当于 `bmm` 运算
   3. 对数输入的 shape 不同的张量, 对应的最后几个维度必须符合矩阵运算规则

#### 3.3 函数详解

**（1）`torch.mm()`**

> `torch.mm()`：计算两个2维张量的矩阵乘法。需要参与操作的两个矩阵都为二维矩阵

**代码示例**

```python
x = t.tensor([[1, 2], [3, 4]])
y = t.tensor([[5, 6], [7, 8]])

result = t.mm(x, y)

print(result)  # 输出 tensor([[19, 22], [43, 50]])
```

上述代码中，使用 `mm()` 函数计算张量 `x` 和 `y` 的矩阵乘法。

**（2）`torch.bmm()`**

> `torch.bmm()`：也就是batched matrix multiply，计算两个3维张量的批量矩阵乘法。需要参与操作的两个矩阵都为三维矩阵，运算方法为在除最高维度外进行内层二维矩阵的点乘运算

**代码示例**

```python
import torch
 
data1 = torch.randint(0, 10, (3, 2, 3), dtype=torch.float32)
data2 = torch.randint(0, 10, (3, 3, 3), dtype=torch.float32)

print(data1)
print(data2)
print(torch.bmm(data1, data2))

# tensor([[[1., 0., 0.],
#          [9., 2., 9.]],
# 
#         [[7., 5., 0.],
#          [8., 8., 8.]],
# 
#         [[8., 1., 6.],
#          [6., 0., 8.]]])
# tensor([[[8., 5., 1.],
#          [1., 8., 1.],
#          [4., 7., 5.]],
# 
#         [[4., 4., 0.],
#          [1., 1., 4.],
#          [3., 1., 5.]],
# 
#         [[3., 5., 9.],
#          [6., 1., 9.],
#          [1., 1., 5.]]])
# tensor([[[  8.,   5.,   1.],
#          [110., 124.,  56.]],
# 
#         [[ 33.,  33.,  20.],
#          [ 64.,  48.,  72.]],
# 
#         [[ 36.,  47., 111.],
#          [ 26.,  38.,  94.]]])
```

**（3）`torch.matmul()`**

> `torch.matmul()`：支持高维矩阵与地位矩阵进行点乘运算，原因为其支持矩阵的广播机制运算，低维矩阵会自动升维后与另一矩阵相乘

**代码示例**

```python
import torch
 
data1 = torch.randint(0, 10, (3, 2, 3), dtype=torch.float32)
data2 = torch.randint(0, 10, (3, 3), dtype=torch.float32)

print(data1)
print(data2)
print(torch.matmul(data1, data2))

# tensor([[[4., 0., 2.],
#          [0., 9., 9.]],
# 
#         [[2., 9., 1.],
#          [0., 7., 7.]],
# 
#         [[9., 4., 5.],
#          [7., 9., 4.]]])
# tensor([[8., 3., 9.],
#         [6., 1., 7.],
#         [8., 9., 8.]])
# tensor([[[ 48.,  30.,  52.],
#          [126.,  90., 135.]],
# 
#         [[ 78.,  24.,  89.],
#          [ 98.,  70., 105.]],
# 
#         [[136.,  76., 149.],
#          [142.,  66., 158.]]])
```

**（4）@操作符**

在Python3.5以后，python支持了@操作符进行矩阵运算，原理与`torch.matmul()`在多数情况下是等价的，***注意在过低版本的Python版本上无法使用本操作符***

**代码示例**

```python
import torch
 
data1 = torch.randint(0, 10, (3, 2, 3), dtype=torch.float32)
data2 = torch.randint(0, 10, (3, 3), dtype=torch.float32)
print(data1)
print(data2)
print(data1 @ data2)

# tensor([[[9., 1., 9.],
#          [4., 6., 0.]],
# 
#         [[6., 4., 7.],
#          [7., 3., 4.]],
# 
#         [[3., 0., 6.],
#          [6., 2., 0.]]])
# tensor([[2., 7., 8.],
#         [6., 2., 3.],
#         [7., 6., 0.]])
# tensor([[[ 87., 119.,  75.],
#          [ 44.,  40.,  50.]],
# 
#         [[ 85.,  92.,  60.],
#          [ 60.,  79.,  65.]],
# 
#         [[ 48.,  57.,  24.],
#          [ 24.,  46.,  54.]]])
```

#### 3.4 完整示例

```python
import torch

# 矩阵运算规则: 矩阵的行分别于另一个矩阵的列中的对应元素相乘再相加
# 1. 使用 @ 运算符
def test01():

# 形状为: 3行2列
    data1 = torch.tensor([[1,2],
                          [3,4],
                          [5,6]])
    # 形状为: 2行2列
    data2 = torch.tensor([[5,6],
                          [7,8]])
    '''
        # 运算过程和对应结果
        [   
            [1*5+2*7=19, 1*6+2*8=22],
            [3*5+4*7=43, 3*6+4*8=50],
            [5*5+6*7=67, 5*6+6*8=78]
        ]
    '''
    data = data1 @ data2
    print(data)

# 2. 使用 mm 函数
def test02():

# 形状为: 3行2列
    data1 = torch.tensor([[1,2],
                          [3,4],
                          [5,6]])
    # 形状为: 2行2列
    data2 = torch.tensor([[5,6],
                          [7,8]])
    data = torch.mm(data1,data2)
    print(data)

# 3. 使用 bmm 函数
def test03():

# 第一个维度:表示批次
    # 第二个维度:多少行
    # 第三个维度:多少列
    data1 = torch.randn(3,4,5) #4行5列
    data2 = torch.randn(3,5,8) #5行8列

data = torch.bmm(data1,data2)
    print(data.shape)

# 4. 使用 matmul 函数
def test04():

# 对二维矩阵进行计算
    data1 = torch.randn(4,5)
    data2 = torch.randn(5,8)
    print(torch.matmul(data1,data2).shape)

# 对三维矩阵进行计算
    data1 = torch.randn(3, 4, 5)  # 4行5列
    data2 = torch.randn(3, 5, 8)  # 5行8列
    print(torch.matmul(data1,data2).shape)

data1 = torch.randn(3, 4, 5)  # 4行5列
    data2 = torch.randn(5, 8)
    print(torch.matmul(data1,data2).shape)

if __name__ == '__main__':
    # test01()
    # test02()
    # test03()
    test04()
```

### 四、指定运算设备

PyTorch 默认会将张量创建在 CPU 控制的内存中, 即: 默认的运算设备为 CPU。也可以将张量创建在 GPU 上, 能够利用对于矩阵计算的优势加快模型训练。

**将张量移动到 GPU 上有三种方法**:

+ 使用 cuda 方法
+ 直接在 GPU 上创建张量
+ 使用 to 方法指定设备

| 指定设备的方式       | 示例代码                                                     | 代码解释                                                   |
| -------------------- | ------------------------------------------------------------ | ---------------------------------------------------------- |
| 使用 `cuda` 方法     | `python data = torch.tensor([10, 20, 30]) ` `data = data.cuda()` | 使用 `cuda()` 方法将张量从 CPU 移动到 GPU。                |
| 在创建张量时指定设备 | `python data = torch.tensor([10, 20, 30], device='cuda:0')`  | 在创建张量时，通过 `device` 参数直接指定设备为 GPU。       |
| 使用 `to` 方法       | `python data = torch.tensor([10, 20, 30])` `data = data.to('cuda:0')` | 使用 `to()` 方法将张量从 CPU 移动到 GPU。                  |
| 使用 `cpu` 方法      | `python data = data.cpu()`                                   | 使用 `cpu()` 方法将张量从 GPU 移动到 CPU。                 |
| 使用 `torch.device`  | `python device = torch.device("cuda" if torch.cuda.is_available() else "cpu")` `tensor = torch.randn(3, 4, 5, device=device)` | 使用 `torch.device` 动态选择设备，并在创建张量时指定设备。 |

**代码示例**

```python
import torch

# 1. 使用 cuda 方法
def test01():

data = torch.tensor([10,20,30])
    print('存储设备:',data.device)

# 将张量移动到 GPU 设备上
    data = data.cuda()
    print('存储设备:', data.device)

# 将张量从GPU再移动到CPU
    data = data.cpu()
    print('存储设备:', data.device)

# 2. 直接将张量创建在指定设备上
def test02():

data = torch.tensor([10,20,30],device='cuda:0')
    print('存储设备:', data.device)

# 使用 cpu 函数将张量移动到 cpu 上
    data = data.cpu()
    print('存储设备:', data.device)

# 3. 使用 to 方法
def test03():

data = torch.tensor([10,20,30])
    print('存储设备:', data.device)

# 使用 to 方法移动张量到指定设备
    data = data.to('cuda:0')
    print('存储设备:', data.device)

# 4. 注意: 存储在不同设备上的张量不能够直接运算
def test04():
    data1 = torch.tensor([10,20,30])
    data2 = torch.tensor([10,20,30],device='cuda:0')

# data1 = data1.cuda()
    # 代码执行报如下错误
    # RuntimeError: expected device cpu but got device cuda:0
    data = data1 + data2
    print(data)
if __name__ == '__main__':
    # test01()
    # test02()
    # test03()
    test04()
```

### 五、常见运算函数

PyTorch 为每个张量封装很多实用的计算函数，例如计算均值、平方根、求和等等

**代码示例**

```python
import torch

data = torch.randint(0, 10, [2, 3], dtype=torch.float64)
print(data)
print('-' * 50)

# 1. 计算均值
# 注意: tensor 必须为 Float 或者 Double 类型
print(data.mean())
print(data.mean(dim=0))  # 按列计算均值
print(data.mean(dim=1))  # 按行计算均值
print('-' * 50)

# 2. 计算总和
print(data.sum())
print(data.sum(dim=0))
print(data.sum(dim=1))
print('-' * 50)

# 3. 计算平方
print(data.pow(2))
print('-' * 50)

# 4. 计算平方根
print(data.sqrt())
print('-' * 50)

# 5. 指数计算, e^n 次方
print(data.exp())
print('-' * 50)

# 6. 对数计算
print(data.log())  # 以 e 为底
print(data.log2())
print(data.log10())
```

**运行结果**

```
tensor([[7., 1., 5.],
        [9., 2., 8.]], dtype=torch.float64)
--------------------------------------------------
tensor(5.3333, dtype=torch.float64)
tensor([8.0000, 1.5000, 6.5000], dtype=torch.float64)
tensor([4.3333, 6.3333], dtype=torch.float64)
--------------------------------------------------
tensor(32., dtype=torch.float64)
tensor([16.,  3., 13.], dtype=torch.float64)
tensor([13., 19.], dtype=torch.float64)
--------------------------------------------------
tensor([[49.,  1., 25.],
        [81.,  4., 64.]], dtype=torch.float64)
--------------------------------------------------
tensor([[2.6458, 1.0000, 2.2361],
        [3.0000, 1.4142, 2.8284]], dtype=torch.float64)
--------------------------------------------------
tensor([[1.0966e+03, 2.7183e+00, 1.4841e+02],
        [8.1031e+03, 7.3891e+00, 2.9810e+03]], dtype=torch.float64)
--------------------------------------------------
tensor([[1.9459, 0.0000, 1.6094],
        [2.1972, 0.6931, 2.0794]], dtype=torch.float64)
tensor([[2.8074, 0.0000, 2.3219],
        [3.1699, 1.0000, 3.0000]], dtype=torch.float64)
tensor([[0.8451, 0.0000, 0.6990],
        [0.9542, 0.3010, 0.9031]], dtype=torch.float64)
```

### 六、其他运算相关函数总结

+ **数学运算**

```python
x.abs()                       # 逐元素取绝对值
x.ceil()                      # 逐元素向上取整
x.floor()                     # 逐元素向下取整
x.round()                     # 逐元素四舍五入
x.exp()                       # 逐元素计算自然常数为底的指数
x.log()                       # 逐元素计算x的自然对数
x.reciprocal()                # 逐元素求倒数
x.square()                    # 逐元素计算平方
x.sqrt()                      # 逐元素计算平方根
x.sin()                       # 逐元素计算正弦
x.cos()                       # 逐元素计算余弦
x.add(y)                      # 逐元素加
x.subtract(y)                 # 逐元素减
x.multiply(y)                 # 逐元素乘（积）
x.divide(y)                   # 逐元素除
x.mod(y)                      # 逐元素除并取余
x.pow(y)                      # 逐元素幂
x.max()                       # 指定维度上元素最大值，默认为全部维度
x.min()                       # 指定维度上元素最小值，默认为全部维度
x.prod()                      # 指定维度上元素累乘，默认为全部维度
x.sum()                       # 指定维度上元素的和，默认为全部维度
```

+ **逻辑运算**

```python
x.isfinite()                  # 判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal_all(y)                # 判断两个Tensor的全部元素是否相等，并返回形状为[1]的布尔类Tensor
x.equal(y)                    # 判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                # 判断两个Tensor的每个元素是否不相等
x.less_than(y)                # 判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               # 判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater_than(y)             # 判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            # 判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 # 判断两个Tensor的全部元素是否接近
```

+ **矩阵运算**

```python
x.t()                         # 矩阵转置
x.transpose([1, 0])           # 交换第 0 维与第 1 维的顺序
x.norm('fro')                 # 矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                # 矩阵（x-y）的2范数
x.matmul(y)                   # 矩阵乘法
```

标签: pytorch

非特殊说明，本博所有文章均为博主原创。

如若转载，请注明出处：https://lilinchao.com/archives/2942.html

上一篇 02.Pytorch张量的创建

下一篇 04.Pytorch张量类型转换

03.Pytorch张量数值计算

评论已关闭

栏目分类

标签云

友情链接申请

03.Pytorch张量数值计算

评论已关闭

 栏目分类

标签云

友情链接申请

栏目分类

标签云

友情链接申请