李林超博客
首页
归档
留言
友链
动态
关于
归档
留言
友链
动态
关于
首页
GO
正文
golang算法篇之kmp算法介绍
Leefs
2024-04-06 PM
3124℃
0条
[TOC] ### 一、题目描述 **LeetCode 28. 找出字符串中第一个匹配项的下标** 给你两个字符串 `haystack` 和 `needle` ，请你在 `haystack` 字符串中找出 `needle` 字符串的第一个匹配项的下标（下标从 0 开始）。如果 `needle` 不是 `haystack` 的一部分，则返回 `-1` 。 **示例 1：** ``` 输入：haystack = "sadbutsad", needle = "sad" 输出：0 解释："sad" 在下标 0 和 6 处匹配。 第一个匹配项的下标是 0 ，所以返回 0 。 ``` **示例 2：** ``` 输入：haystack = "leetcode", needle = "leeto" 输出：-1 解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。 ``` ### 二、字符串匹配暴力法 #### 2.1 示例 通过下方示例数据对字符串匹配做讲解 ``` 输入：text = "abaacababcac", pattern = "ababc" 输出：5 ``` #### 2.2 解析 一般的字符串匹配解法是将 2 个串的字符进行挨个比较，相当于是把每个字符都比较了一遍，这样是一定能得到结果的，不过显然这样操作导致的时间复杂度是`O(m*N)`,也就是 2 个字符串的长度之积，俗称暴力解法。 **用图像表示暴力解法的过程如下**： + 一开始，i 和 j 分别指向主字符串和子字符串 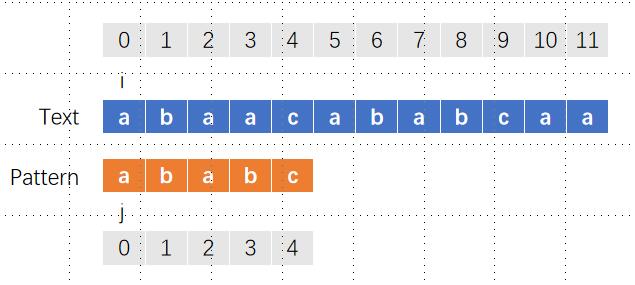 + 这个时候开始比较 `t[i]` 和 `p[j]`，如果匹配则 i 和 j 同时向右移动一格，这样 i 和 j 同时移动到了位置 3  + 此时 i 和 j 不匹配了，需要对 i 和 j 进行回退，i 回退到了它最开始的下一位置，即位置 1，而 j 回退到位置 0  + 此时 i 和 j 仍然不匹配，i 继续向右移动一格，即位置 2，j 依然保持位置 0  + 如此反复，每当不匹配时，i 都会回到开始匹配的位置同时移动一格，而 j 回到位置 0，当匹配时，i 和 j 同时向右移动，直到 j 到达子字符串的末尾。   #### 2.3 实现代码 ```go /** 步骤: 1. 获取字符串长度 2. 将字符串转换成字符数组 3. 遍历字符数组,进行比较 */ func strStr(haystack string, needle string) int { L := len(needle) // 第二个字符串的长度 Cap := len(haystack) // 带比较字符串的长度 H := []byte(haystack) // 将字符串转换成 byte 数组 N := []byte(needle) for i, val := range H { if val == N[0] { if i+L <= Cap && haystack[i:i+L] == needle { return i } } } return -1 } ``` ### 三、KMP算法原理 #### 3.1 概述 KMP 算法则用了一种聪明的办法，当发现字符串不匹配的时候，并不会从头开始比较，因为之前已经匹配成功的字符可以给我们提供一些有用的信息，利用这个信息可以将子串移动到某个位置，并从这个位置直接开始比较，它的时间复杂度降到了`O(m+n)`，也就是 2 个字符串的长度之和。 #### 3.2 字符串的前缀和后缀 首先需要知道字符串的前缀和后缀： 对于字符串 `ababc` 来说，它的前缀有 `[a,ab,aba,abab]`，也就是以字符串第一个字符作为开头，同时不包括最后一个字符的所有子串。 同理它的后缀有 `[c,bc,abc,babc]`，也就是以字符串最后一个字符作为结尾，同时不包括第一个字符的所有字串。 #### 3.3 字符串的最长公共前后缀 了解了这个，我们再来说什么是字符串的**最长公共前后缀**，说白了，也就是前缀和后缀这 2 个集合中的相同部分，同时取最长的那个，就是这个字符串的**最长公共前后缀**。 显然，在这个例子中，`ababc` 是没有公共前后缀的。但是对于 `abab`，它的前缀和后缀分别是 `[a,ab,aba]` 和 `[b,ab,bab]`，那么它的**最长公共前后缀**就是 `ab`。 现在，我们的目标就是取得 `ababc` 所有子串 `[a,ab,aba,abab,ababc]` 的**最长公共前后缀**的长度，分别保存在 `next` 数组中，我们只要知道最大长度即可，并不用关心串具体是什么，而我们目前通过观察即可得出 next 数组这里是 `[0,0,1,2,0]`，我们先知道这个结果即可，此计算方法后续会说明。 #### 3.4 KMP的思路分析 + 得到这个有什么用，回到刚刚的例子，当我们第一次碰到不匹配时（i 和 j 都等于 3 的时候）：  此时 i 和 j 之前的 3 个字符 `aba` 必然完全匹配的，因为只有前面匹配成功了 j 才能走到 3，而我们又知道 `aba` 的**最长公共前后缀**是 `a`。 这可以给我们一个很好的提示，**主串中的 `aba` 的后缀和字串中的 `aba` 前缀有最长的公共部分 `a`**，这样一来，我们就没必要重新比较了，直接将相同部分对齐就好了 + 也就是说让 j 退回到位置 1 就可以了，而 i 保持不变。  **分析一下，为什么 j 知道应该退回到位置 1**： 1. 我们知道 j 是在位置 3 不匹配的，那么 j 前面的字符串我们可以知道是 `aba` 2. 前面我们已经得到了 next 数组，知道 `aba` 的最长公共前后缀长度是 **1** 3. 也就是说，我们可以知道 i 之前 **1** 个位置（主串的后缀）和子串开头之后 **1** 个位置（子串的前缀）是相同的 4. 进而我们可以让相同部分对齐，也就是让 `j=next[j-1]` + 接下来，我们发现 i 和 j 仍然不匹配，而 j 之前的字符 `a` 最长公共前后缀是 0，此时 j 退到位置 0，i 仍然保持不变。  + 接下来 i 和 j 匹配，同时右移一格  + 此时 i 和 j 不匹配，`j=next[j-1]` 回退到 0，然后我们发现 i 和 j 仍然不匹配，同时 j 已经是 0 了，那么我们就让 i 往右移动一格。   可以看到，相比于暴力解法，i 始终在前进，并没有后退（顶多保持不变），然后我们通过 next 数组来改变 j 的值。 #### 3.5 求解字符串最长公共前后缀 最后，我们还剩下一个问题，如何求 next 数组，也就是求模式字符串各个子串的最长公共前后缀长度。 我们先初始化一个和模式字符串长度相等的 next 数组，在 next 数组中，第 1 位默认为 0，因为我们规定只有一个字符的字符串没有前缀和后缀，自然公共前后缀长度只能是 0。 我们依然设定 2 个指针 i 和 j，j 指向位置 0，i 从位置 1 开始依次为 next 数组进行赋值  我们可以把这个过程依然看作是 2 个字符串的比较，j 指向的是模式字符串的前缀，而 i 指向的是模式字符串的后缀  和上面的字符串匹配一样，我们执行同样的处理： 1. 当 i 和 j 匹配时，i 和 j 同时右移一格 2. 当 i 和 j 不匹配时，如果 j 不在字符串开头（位置 0），就回退到上一个能匹配到的位置 3. 当 i 和 j 不匹配时，如果 j 在字符串开头（位置 0），那么 i 就右移一格 **对 next [1] 赋值**：i 和 j 不匹配，同时 j 已经是字符串开头，赋值 0  对 next [2] 赋值，i 和 j 匹配，此时 j 为 0，代表只有 1 个字符匹配 (j+1)，赋值 1  对 next [3] 赋值，i 和 j 匹配，此时 j 为 1，代表有 2 个字符匹配 (j+1)，赋值 2  对 next [4] 赋值，i 和 j 不匹配，此时 j 为 2，可以得知 j 前面的字符是 `ab`，而 `ab` 的最长公共前后缀长度就是 `next[1]`，这个值我们前面已经求得了结果是 0，所以 j 回退到位置 0，用代码表示就是 `j=next[j-1]`  此时 i 和 j 仍然不匹配，但是 j 已为 0，无法继续回退，所以直接对 next [4] 赋值为 0  实际上，我们在求解模式字符串 `ababc` 的最长公共前后缀长度的时候，不可避免的会对它的子串进行求解，这样可以方便在不匹配时进行回退，这也是动态规划的思想，要求的结果可以用先前已经求得的结果得出。而我们本身就是要对模式字符串的各个子串进行求解，所以可谓一举两得。 #### 3.6 代码实现 ```go // 方法二 KMP算法 // 此函数用来初始化next数组 func initNext(needle string) []int { //记录后缀中末尾 abc中c i := 1 //前缀中末尾;同时在这里也有着记录最长公共串长度的作用，二者本质是一样的 j := 0 L := len(needle) //初始化next数组；next[0]默认为0，因为对于一个字母我们不认为其具有前后缀，后续也不会再对next[0]进行赋值 next := make([]int, L) //求next数组过程中，我们的i不回退，采用类似于动态规划的思想，也是我们这里的循环条件 for i < L { //如果前后缀匹配 if needle[i] == needle[j] { // 如果字符串对应的编码值相同 //前缀末尾向后移一位，同时代表长度+1 j++ //当前后缀末尾所在位置的最长子串即为j //最长子串是有基础的，如果next[2]=2，那么next[3]的可能性为3或者0,这里是为3的情况 next[i] = j //后缀末尾向后移一位 i++ } else { //如果前后缀不匹配 //当j>0，说明仍旧处于回退的过程 if j > 0 { j = next[j-1] } else { //如果j=0，并且前后缀依旧不匹配，则长度计数应该重新从0开始 //这里是为0的情况 next[i] = j //后缀末尾向后移 i++ } } } //返回next数组 return next } // kmp算法，用空间换时间 func strStr(haystack string, needle string) int { //获取next数组 next := initNext(needle) //主串长度 L := len(haystack) //目标匹配长度，即needle的长度 target := len(needle) //匹配字符串中指针位置 j := 0 //i为主串中指针的位置 for i := 0; i < L; { // 如果匹配上了 if haystack[i] == needle[j] { if j == target-1 { return i - target + 1 } j++ i++ } else { //如果没匹配上 //跟计算next数组有异曲同工之妙 if j > 0 { j = next[j-1] } else { i++ } } } return -1 } func main() { str1and := "aaaabbb" str2and := "abb" num := strStr(str1and, str2and) fmt.Println(num) } ``` ### 四、题目二 #### 4.1 题目描述 **LeetCode 459. 重复的子字符串** 给定一个非空的字符串 `s` ，检查是否可以通过由它的一个子串重复多次构成。 **示例 1:** ``` 输入: s = "abab" 输出: true 解释: 可由子串 "ab" 重复两次构成。 ``` **示例 2:** ``` 输入: s = "aba" 输出: false ``` **示例 3:** ``` 输入: s = "abcabcabcabc" 输出: true 解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。) ``` #### 4.2 代码实现 ```go /** 方法一:字符串拼接法 思路 新建一个新字符串str=s+s，把str的首元素和尾元素去掉，剩下的部分如果还含有s，则返回true。 */ func repeatedSubstringPattern2and(s string) bool { var str1 string = s + s var str2 string = str1[1 : len(str1)-1] // 去掉首/尾字母 if strings.Contains(str2, s) { return true } else { return false } } func repeatedSubstringPattern3and(s string) bool { var str1 string = s + s var str2 string = str1[1 : len(str1)-1] // 去掉首/尾字母 return strings.Contains(str2, s) } func repeatedSubstringPattern4and(s string) bool { var str1 string = s + s return strings.Contains(str1[1:len(str1)-1], s) } /** 方法二 暴力解法 */ func repeatedSubstringPattern5and(s string) bool { L := len(s) record := false for i := 1; i < L/2+1; i++ { if L%i != 0 { continue } num := L / i for ; num > 0; num-- { if s[:i] != s[(num-1)*i:num*i] { record = false break } record = true } if record == true { return record } } return record } /** KMP算法 正是因为 最长相等前后缀的规则，当一个字符串由重复子串组成的，最长相等前后缀不包含的子串就是最小重复子串。 */ // 前缀表(不减一)的代码实现 func repeatedSubstringPattern6and(s string) bool { n := len(s) if n == 0 { return false } j := 0 // 初始化 next 数组 // next 数组中存储最长公共后缀部分,跳过第一个公共前缀项 next := make([]int, n) next[0] = j // for i := 1; i < n; i++ { // 匹配不成功,j回到前一位置 next数组所对应的值 for j > 0 && s[i] != s[j] { j = next[j-1] } // 匹配成功,j忘后移 if s[i] == s[j] { j++ } // 更新 next 数组的值 next[i] = j } // 最后判断是否是重复的子字符串 // next[n-1] 最长相同前后缀的长度 // n-next[n-1] === n - 最长相同前后缀长度 == 最小相同前后缀长度 // next[n-1] != 0 字符串中存在相同前后缀 if next[n-1] != 0 && n%(n-next[n-1]) == 0 { return true } return false } // 这里使用前缀表统一减一的实现方式 func repeatedSubstringPattern7and(s string) bool { n := len(s) if n == 0 { return false } next := make([]int, n) j := -1 next[0] = j for i := 1; i < n; i++ { for j >= 0 && s[i] != s[j+1] { j = next[j] } if s[i] == s[j+1] { j++ } next[i] = j } // next[n-1]+1 最长相同前后缀的长度 if next[n-1] != -1 && n%(n-(next[n-1]+1)) == 0 { return true } return false } func main() { str := "abcabcabc" //str2 := "abcabcabca" bl := repeatedSubstringPattern6and(str) //blr := repeatedSubstringPattern4and(str2) fmt.Println(bl) //fmt.Println(blr) } ``` *附参考原文链接地址* *https://www.xdull.cn/kmp.html*
标签:
Golang
非特殊说明，本博所有文章均为博主原创。
如若转载，请注明出处：
https://www.lilinchao.com/archives/2898.html
上一篇
golang之gorm操作示例并兼容达梦数据库
下一篇
golang算法篇之0-1背包算法介绍
取消回复
评论啦~
提交评论
栏目分类
随笔
2
Java
326
大数据
229
工具
31
其它
25
GO
48
NLP
8
标签云
字符串
FastDFS
容器深入研究
Thymeleaf
递归
数学
Golang
BurpSuite
Jenkins
数据结构
人工智能
ajax
算法
SpringBoot
GET和POST
查找
Http
Java编程思想
Java
Spring
ClickHouse
Redis
Livy
Azkaban
Beego
FileBeat
JavaWEB项目搭建
Stream流
锁
NIO
友情链接
申请
范明明
庄严博客
Mx
陶小桃Blog
虫洞